Naive Bayes VS Maximum Entropy
- Maximum Entropy Recap
- Model detail about ME
- Naive Bayes TO Maximum Entropy
Maximum Entropy Recap
Maximum Entropy Model:
$H(y|x)=-\sum_{x,y\in\mathcal{Z}=\mathcal{X}\times\mathcal{Y}}p(y,x)log[p(y|x)]$
$p^*(y|x)=argmax_{p(y|x)\in P}H(y|x)$
$p(y|x)=\frac{1}{Z(x)}exp[\sum_{k=1}^K\theta_kf_k(y,x)]$
Maximum Entropy Markov Model
$p_{MEMM}(y|x)=\prod_{t=1}^{T}p(y_t|y_{t-1},x)$
$p(y_t|y_{t-1},X)=\frac{1}{Z_t(y_{t-1},X)}exp[\sum_{k=1}^{K}\theta_kf_k(y_t,y_{t-1},X)]$
HMM vs MEMM
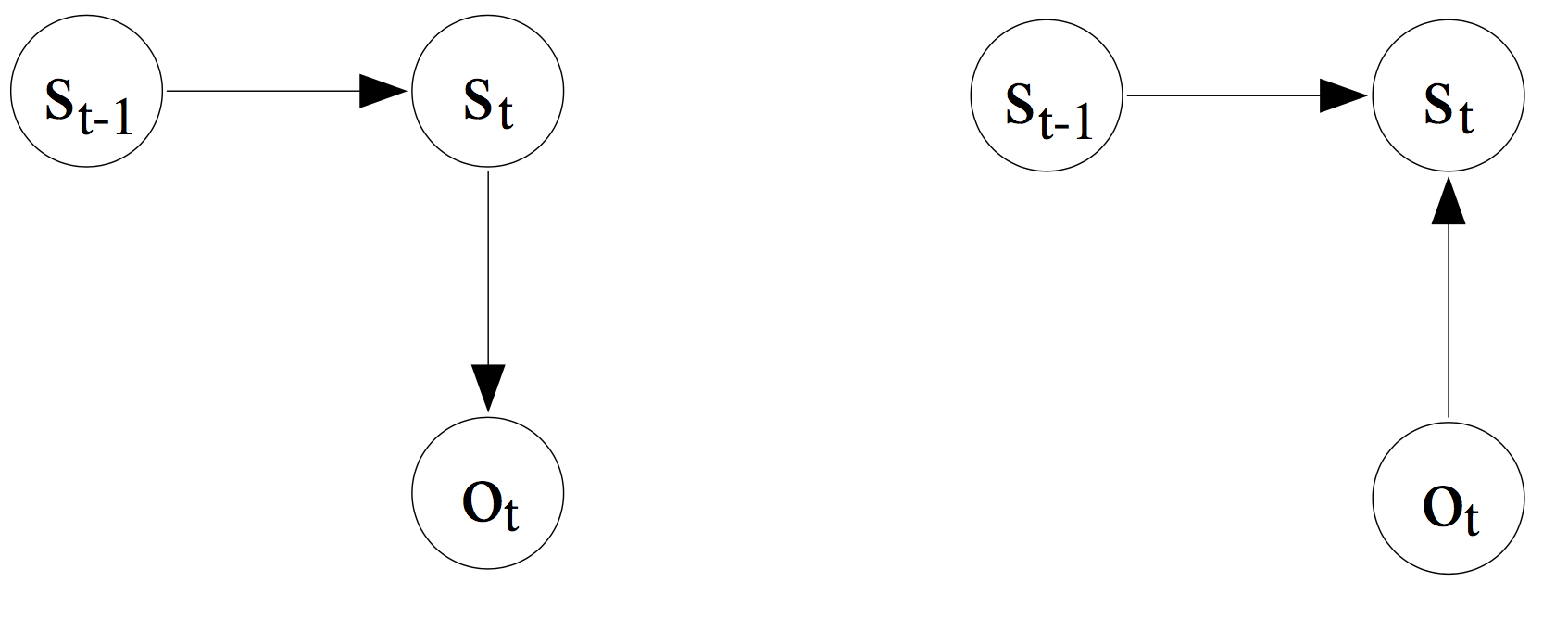
More on MEMM
In the Maximum Entropy Markov Models the transition and observation functions (i.e., the HMM matrices $A$ and $B$ ) are replaced by a single function:
$P(s_{t} \mid s_{t-1}, o_{t})$
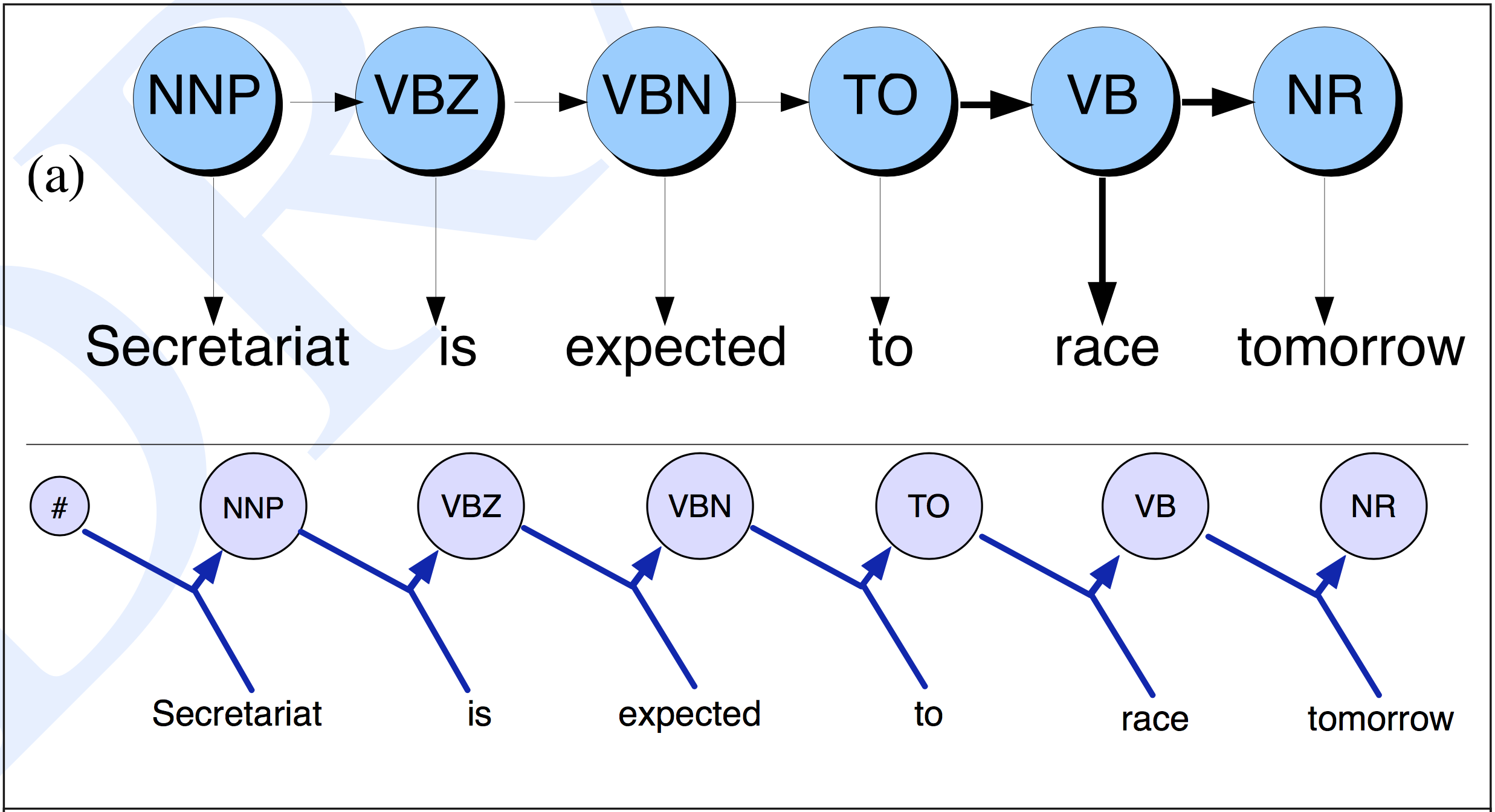
- HMM: current observation only depends on the current state
- MEMM: may also depend on the previous state, $P(s_{t} \mid s_{t-1}, o_{t})$
- HMM: distinct probability estimates for each transition and observation
- MEMM: one transition probability matrix which encapsulates all combinations of previous states $S_{t−1}$ and current observation $O_t$ pairs in the training data to the current state $S_t$
NB条件化就是逻辑回归
对于随机变量$X = X_i,i = 1,2,…$,预测变量$Y$为Bernoulli分布,参数$\pi=P(Y=1)$
对于每一个$X_i,P(X_i|Y_k)\sim N(\mu_{ik},\sigma_i^2)$
对于$i\neq j,X_i与X_j$在给定$Y$的情况下条件无关
在二分类的情况下,贝叶斯公式可以写成: $$P(Y=1|X)=\frac{P(Y=1)P(X|Y=1)}{P(Y=1)P(X|Y=1)+P(Y=0)P(X|Y=0)}$$ $$P(Y=1|X)=\frac{1}{1+\frac{P(Y=0)P(X|Y=0)}{P(Y=1)P(X|Y=1)}}$$ $$P(Y=1|X)=\frac{1}{1+exp(ln\frac{P(Y=0)P(X|Y=0)}{P(Y=1)P(X|Y=1)})}$$
$$P(Y=1|X)=\frac{1}{1+exp(ln\frac{P(Y=0)}{P(Y=1)}+\sum_i ln\frac{P(X_i|Y=0)}{P(X_i|Y=1)})}$$
由于$P(X_i|Y=y_k)$成高斯分布, $$\sum_i ln\frac{P(X_i|Y=0)}{P(X_i|Y=1)}=\sum_i ln\frac{\frac{1}{\sqrt{2\pi\sigma_i^2}}exp(\frac{-(X_i-\mu_{i0})^2}{2\sigma_i^2})}{\frac{1}{\sqrt{2\pi\sigma_i^2}}exp(\frac{-(X_i-\mu_{i1})^2}{2\sigma_i^2})}$$ $$=\sum_i ln[exp(\frac{(X_i-\mu_{i1})^2-(X_i-\mu_{i0})^2}{2\sigma_i^2})]$$ $$=\sum_i (\frac{\mu_{i0}-\mu_{i1}}{\sigma_i^2}X_i+\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2})$$
最后得到,$$P(Y=1|X)=\frac{1}{1+exp(ln\frac{1-\pi}{\pi}+\sum_i (\frac{\mu_{i0}-\mu_{i1}}{\sigma_i^2}X_i+\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2}))}$$
进而,$$P(Y=1|X)=\frac{1}{1+exp(w_0+\sum_iw_iX_i)}$$
其中,$$w_0=ln(\frac{1-\pi}{\pi})+\sum_i\frac{\mu_{i1}^2-\mu_{i0}^2}{2\sigma_i^2}$$ $$w_i=\frac{\mu_{i0}-\mu_{i1}}{\sigma_i^2}$$