非线性降维

  • MDS
  • Kernel PCA
  • 流形学习

MultiDimension Scaling

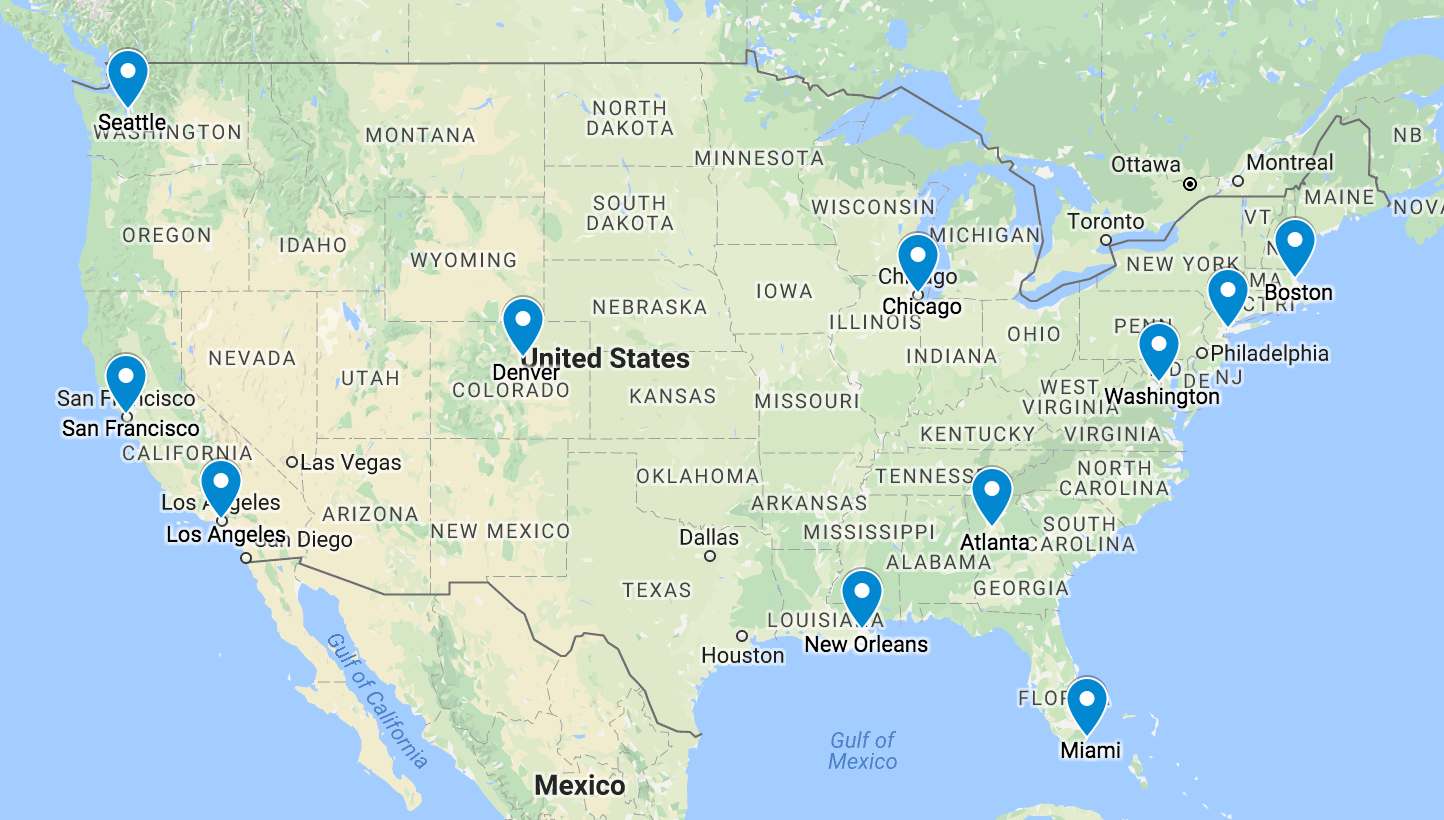
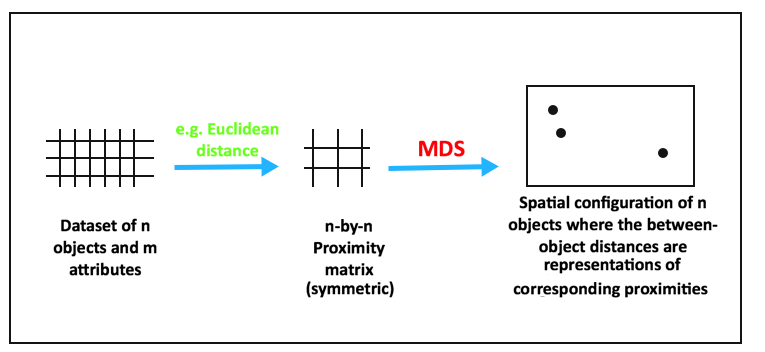
MDS的目标是在降维的过程中将数据的dissimilarity(差异性)保持下来，也可以理解降维让高维空间中的距离关系与低维空间中距离关系保持不变.

流形学习

  • ISOMAP
  • LLE
  • TSNE

ISOMAP 等度量映射

  • Geodesic Distances
  • Shortest Path
  • 高时间复杂度

局部线性嵌入(LLE)

假设每个一样本都与其近邻组成一个线性子空间中

把所有这些子空间连接在一起

t-Distributed Stochastic Neighbor Embedding (t-SNE)

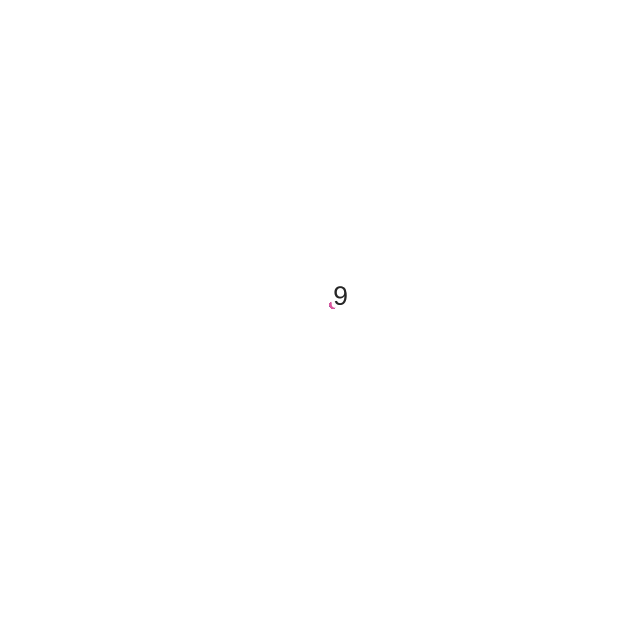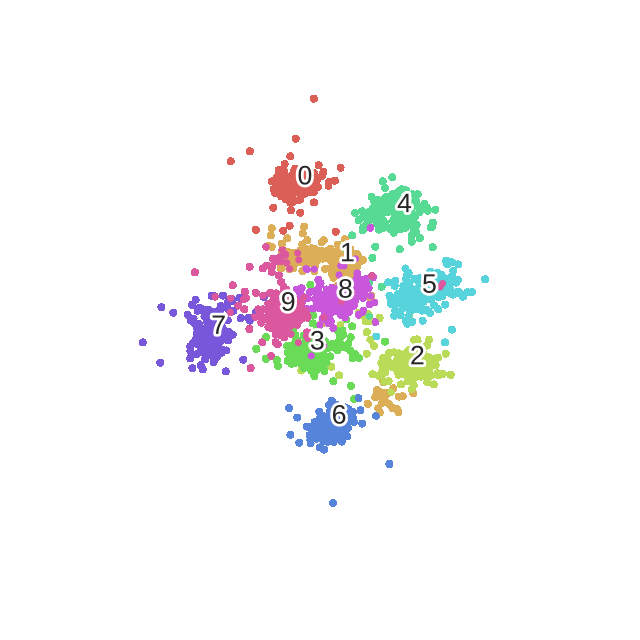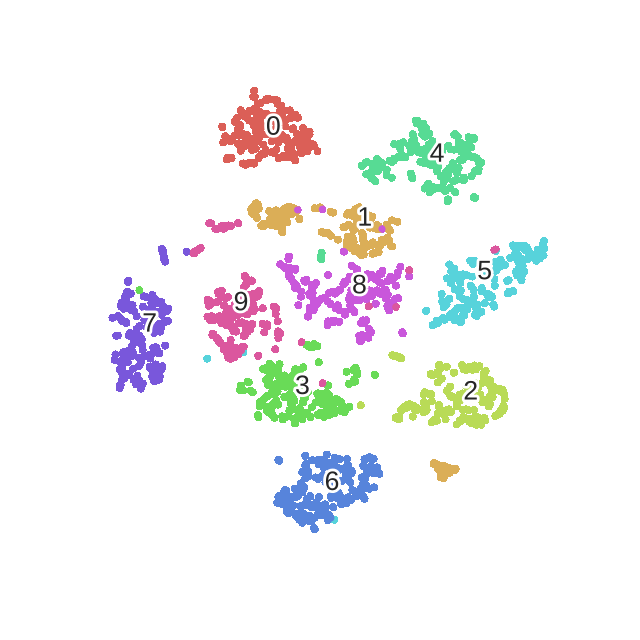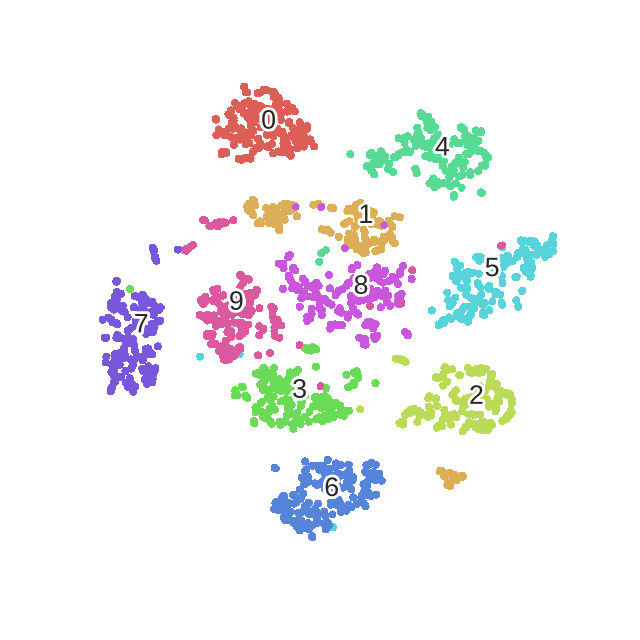
  • $p_{j|i} = \frac{\exp\left(-\left| x_i - x_j\right|^2 \big/ 2\sigma_i^2\right)}{\displaystyle\sum_{k \neq i} \exp\left(-\left| x_i - x_k\right|^2 \big/ 2\sigma_i^2\right)}$
  • $p_{ij} = \frac{p_{j|i} + p_{i|j}}{2N}$
  • $q_{ij} = \frac{f(\left| x_i - x_j\right|)}{\displaystyle\sum_{k \neq i} f(\left| x_i - x_k\right|)} \quad \textrm{with} \quad f(z) = \frac{1}{1+z^2}$
  • $KL(P||Q) = \sum_{i, j} p_{ij} \, \log \frac{p_{ij}}{q_{ij}}.$
  • $\frac{\partial \, KL(P || Q)}{\partial y_i} = 4 \sum_j (p_{ij} - q_{ij}) g\left( \left| x_i - x_j\right| \right) u_{ij} \quad \textrm{where} \, g(z) = \frac{z}{1+z^2}.$
  1. 测量$x_j$到$x_i$的概率距离，认为$x_i$服从高斯分布
  2. 使其具备距离属性
  3. 定义其在映射空间的距离，认为服从自由度为1的$t$分布
  4. 损失函数为这两个距离矩阵的KL散度
  5. 采用梯度下降使损失函数最小
Machine Learning Applications and practices