深度神经网络
- Basic Introduction
- Views on DNN
- RGLM
Basic Introduction
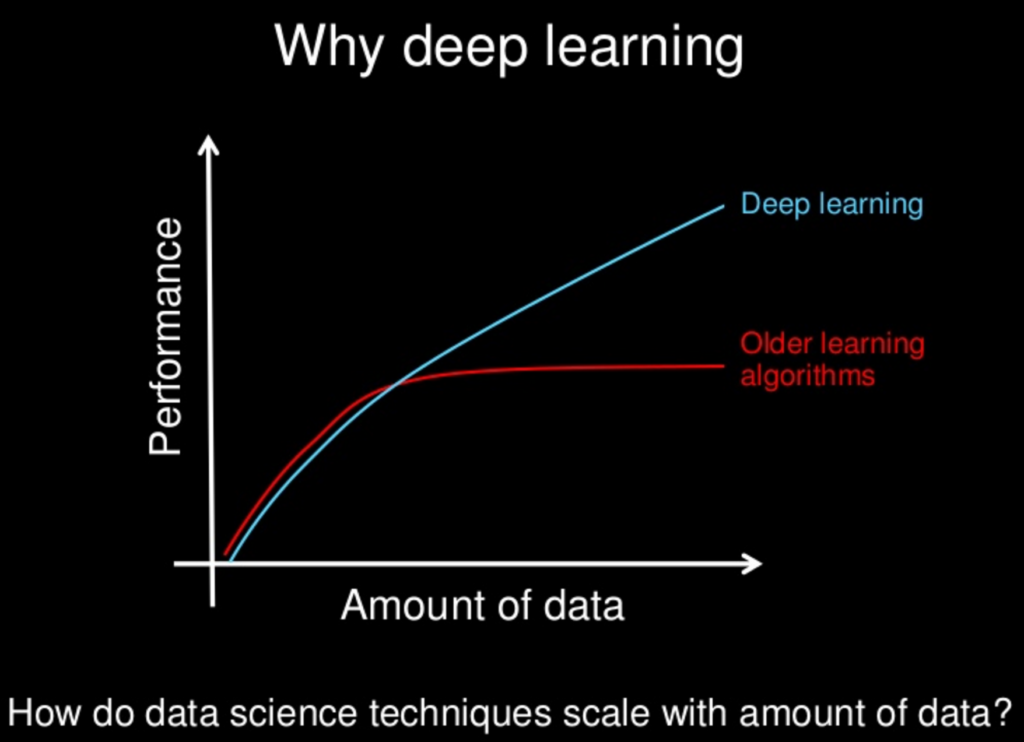

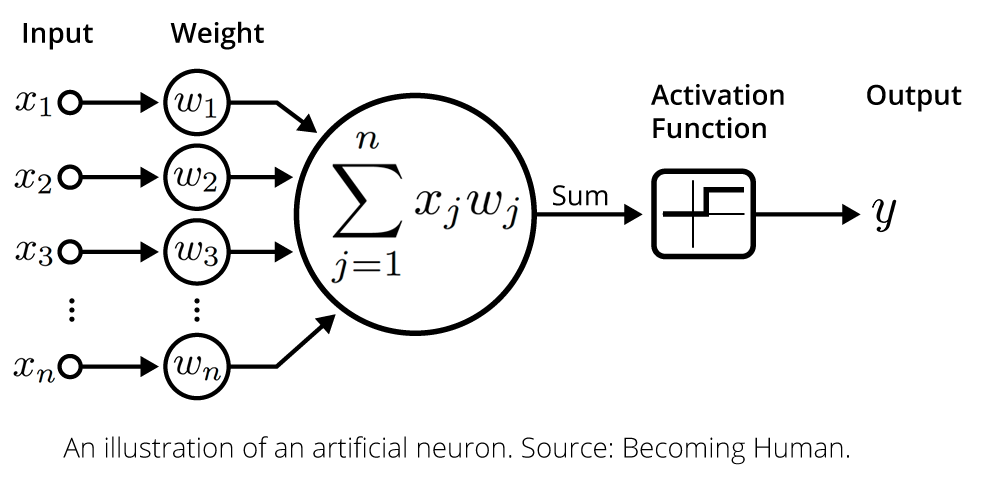
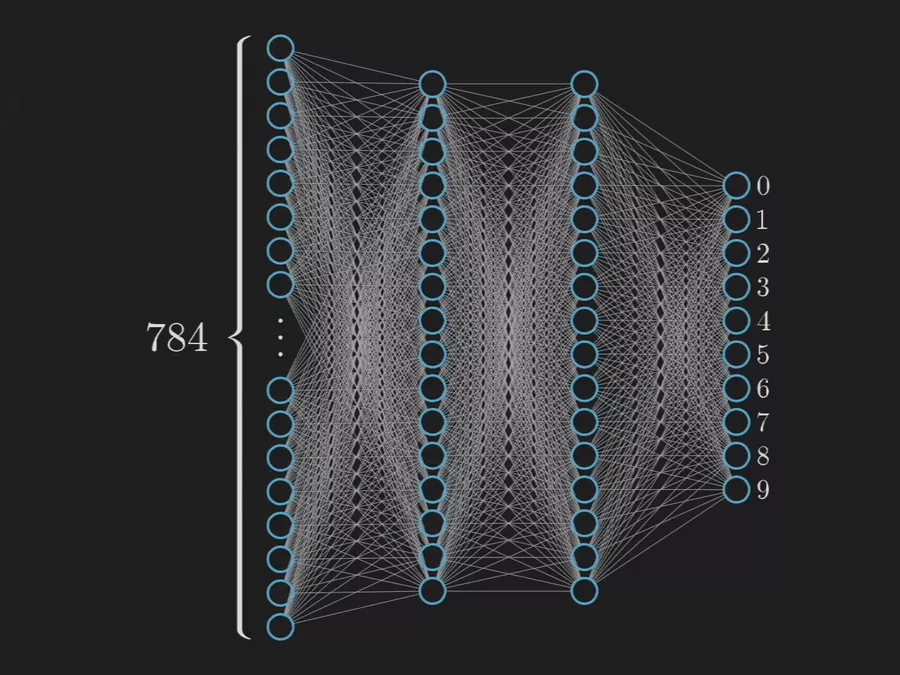
Views On DNN
- High Cost on training a DNN
- Active Function brings non-linearity
- Automatic Feature Learning / Dimension Reduction
- High VC dimensions, which means need control overfitting
- Most used in unstructured data
RGLM
Recursive Generalised Linear Model
A Simple Linear Model
$\eta = \beta^\top x + \beta_0$
$y = \eta+\epsilon \qquad \epsilon \sim \mathcal{N}(0,\sigma^2)$
- $\eta$ is the systematic component of the model
- $\epsilon$ is the random component
Generalised linear models (GLMs)
Extend linear model to problems where the distribution on the targets is not Gaussian but some other distribution (typically a distribution in the exponential family)
$\eta = \beta^\top x, \qquad \beta=[\hat \beta, \beta_0], x = [\hat{x}, 1]$
$\mathbb{E}[y] = \mu = g^{-1}(\eta)$
$g(·)$ is the link function
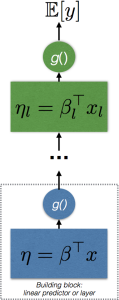
What RGLM means?
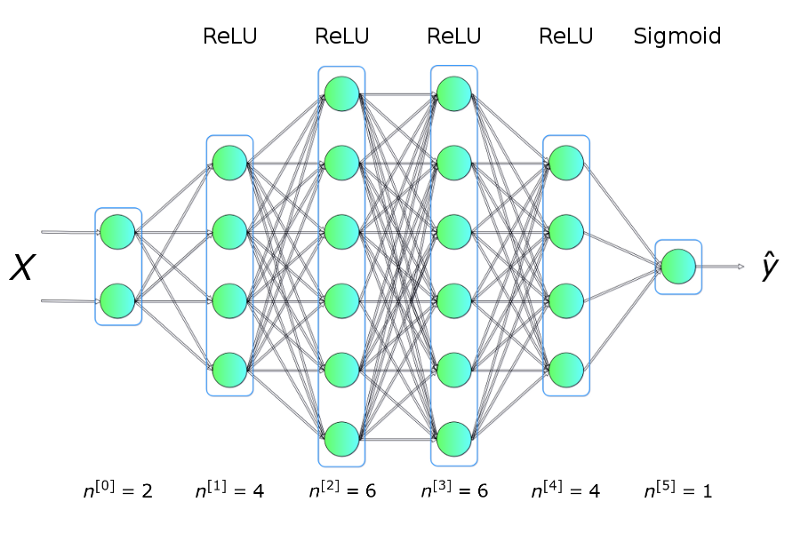
- In deep learning, the basic building block is called a layer.
- Building block can be easily repeated to form more complex, hierarchical and non-linear regression functions
$h_l(x) = f_l(\eta_l)$
$\mathbb{E}[y] = \mu_L = h_L \circ \ldots \circ h_1 \circ h_o(x)$
$\mathcal{L} = - \log p(y | \mu_L)$
* More Detail on DNN *
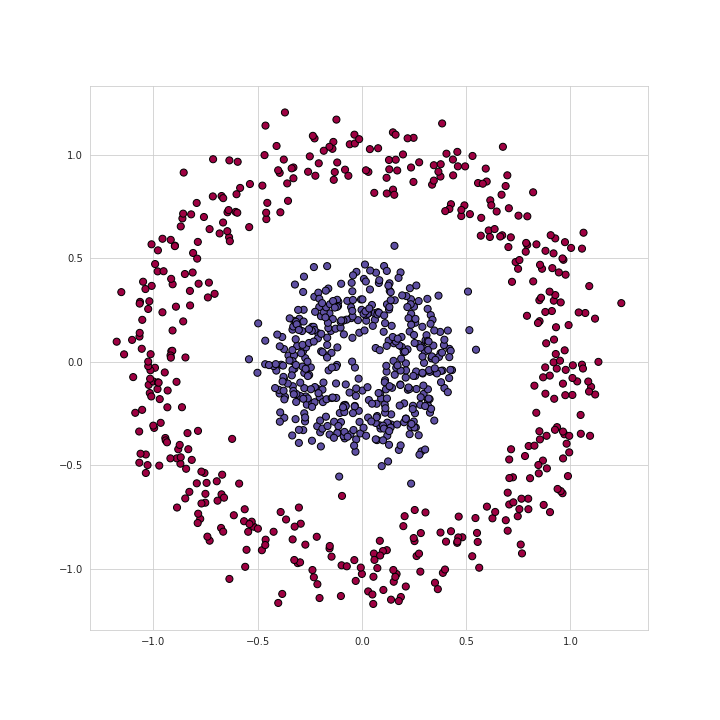
Dataset
NN
Training
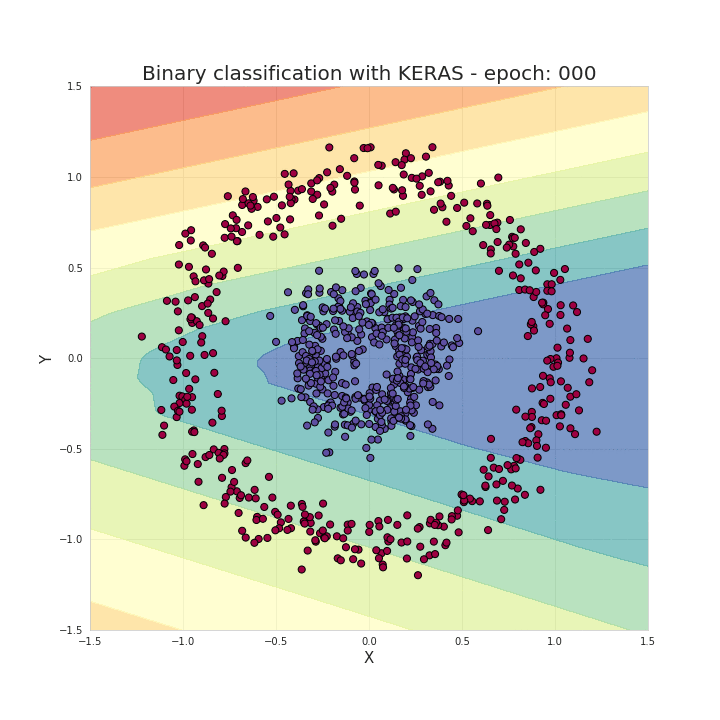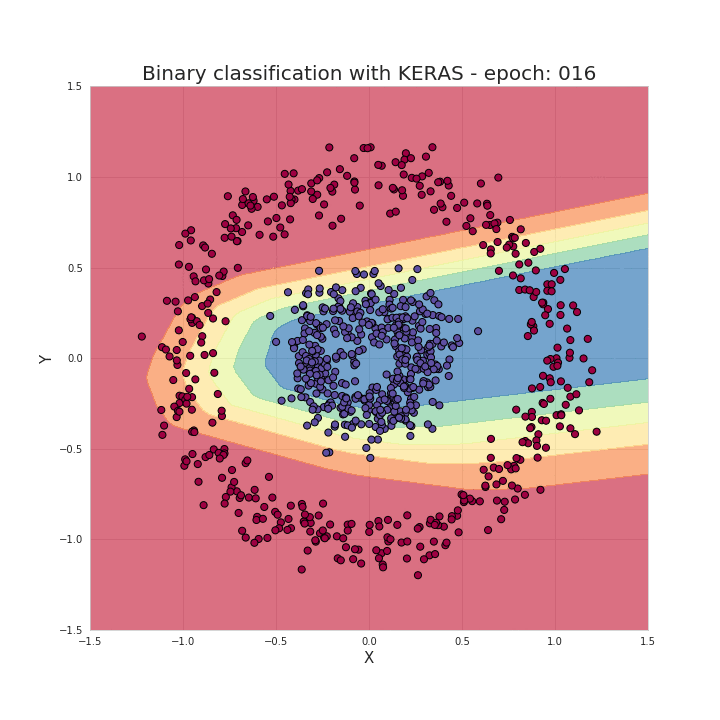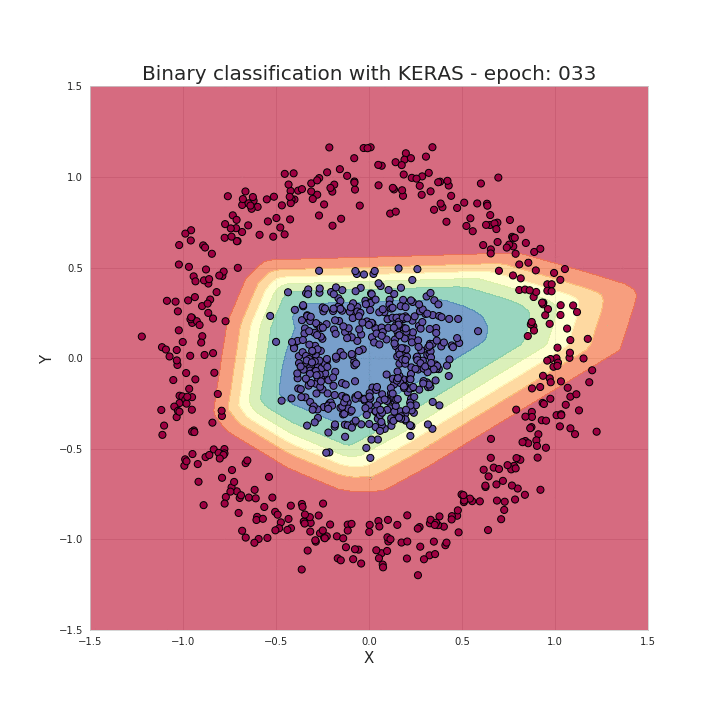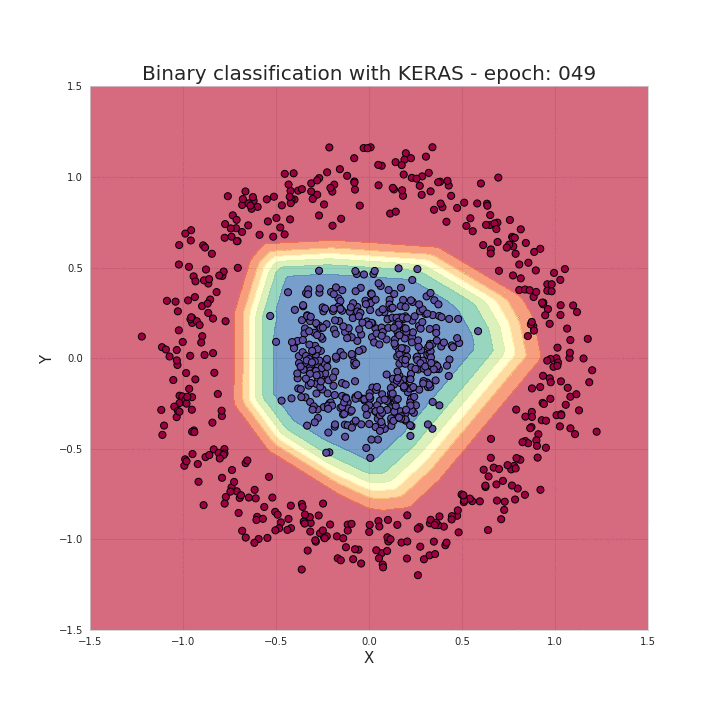
Single neuron operation
Single Layer
$z_i^{[l]}=w_i^T\cdot a^{[l-1]}+b_i, \ \ \ a_i^{[l]}=g^{[l]}(z_i^{[l]})$
$z_1^{[2]}=w_1^T\cdot a^{[1]}+b_1, \ \ \ a_1^{[2]}=g^{[2]}(z_1^{[2]})$
$z_2^{[2]}=w_2^T\cdot a^{[1]}+b_2, \ \ \ a_2^{[2]}=g^{[2]}(z_2^{[2]})$
$z_3^{[2]}=w_3^T\cdot a^{[1]}+b_3, \ \ \ a_3^{[2]}=g^{[2]}(z_3^{[2]})$
$z_4^{[2]}=w_4^T\cdot a^{[1]}+b_4, \ \ \ a_4^{[2]}=g^{[2]}(z_4^{[2]})$
$z_5^{[2]}=w_5^T\cdot a^{[1]}+b_5, \ \ \ a_5^{[2]}=g^{[2]}(z_5^{[2]})$
$z_6^{[2]}=w_6^T\cdot a^{[1]}+b_6, \ \ \ a_6^{[2]}=g^{[2]}(z_6^{[2]})$
Matrix Operation
Vectorizing across multiple examples
Activation function
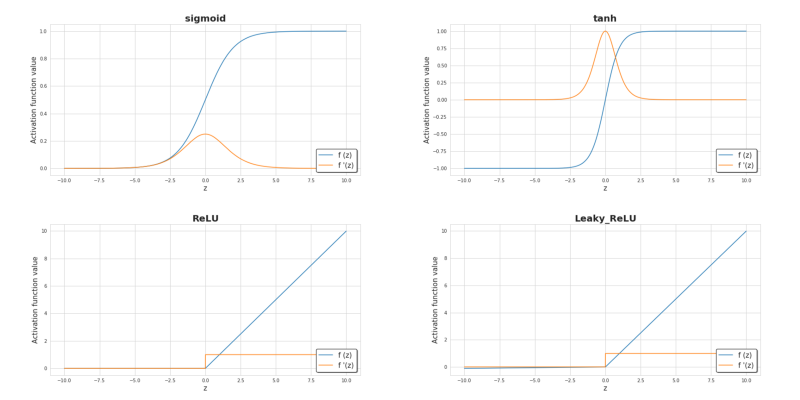
Loss Function
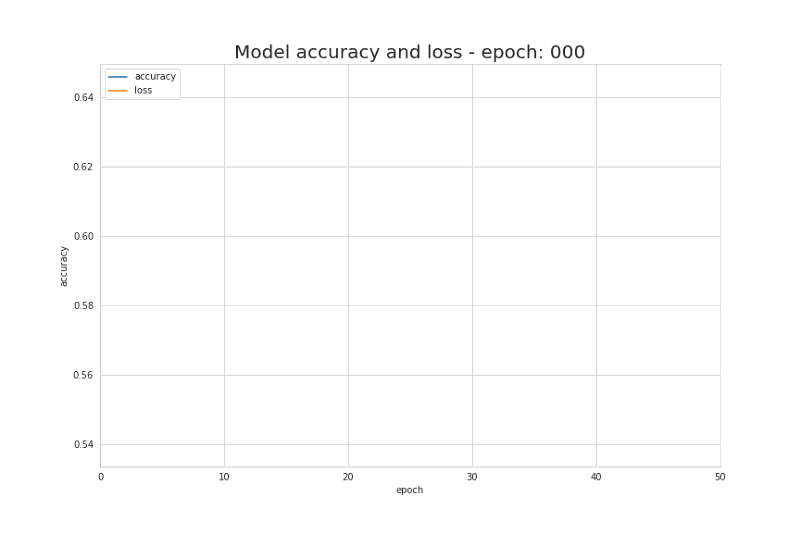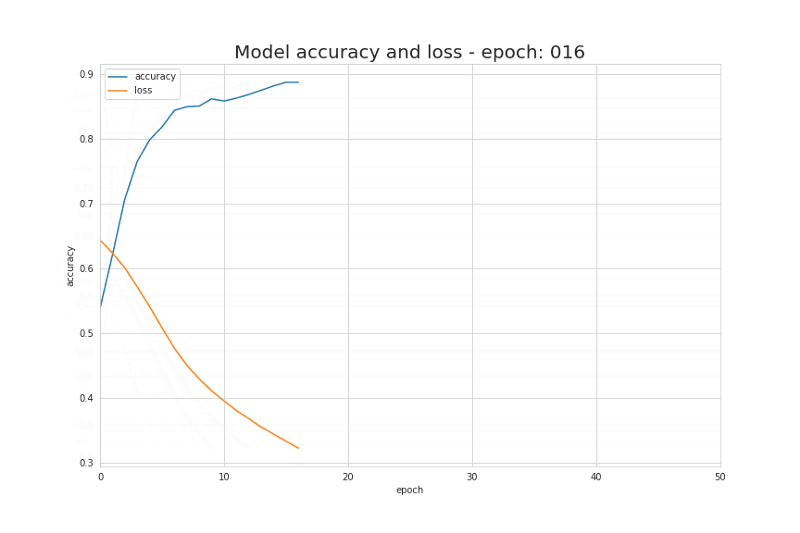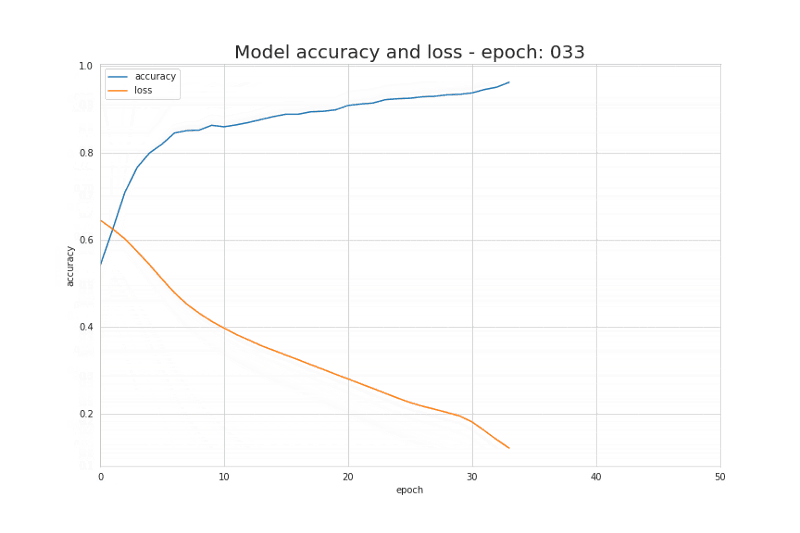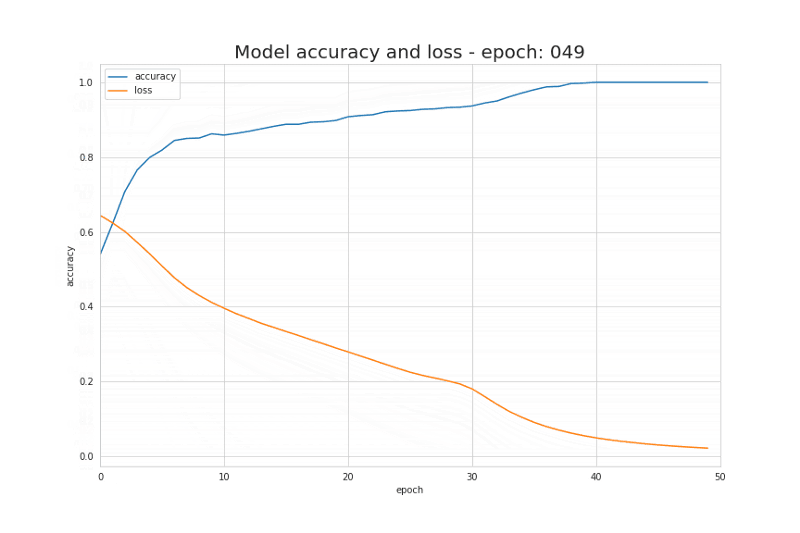
$J(W,b)=\frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})$
$L(\hat{y},y)=-(ylog(\hat{y})+(1-y)log(1-\hat{y}))$
Preventing Overfitting
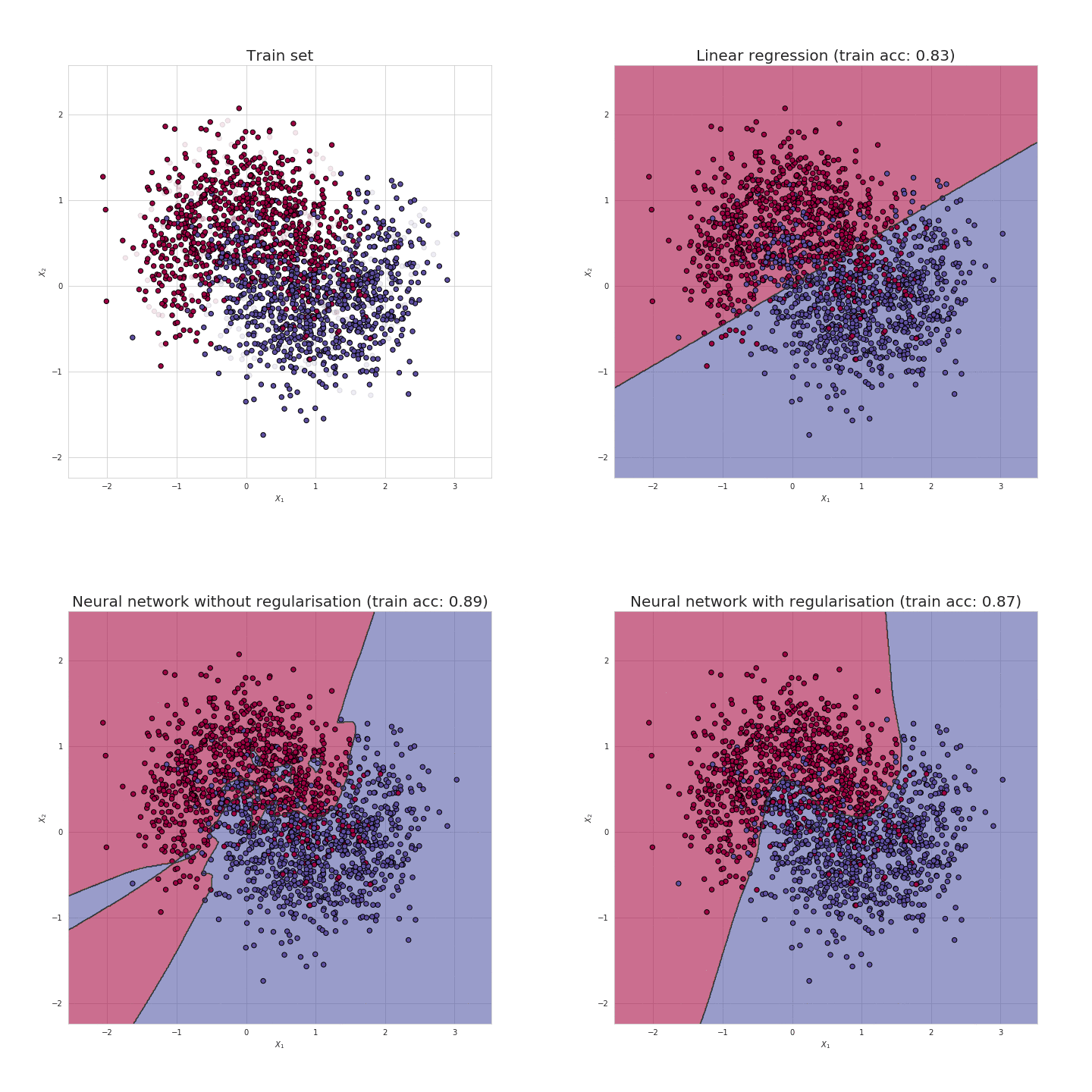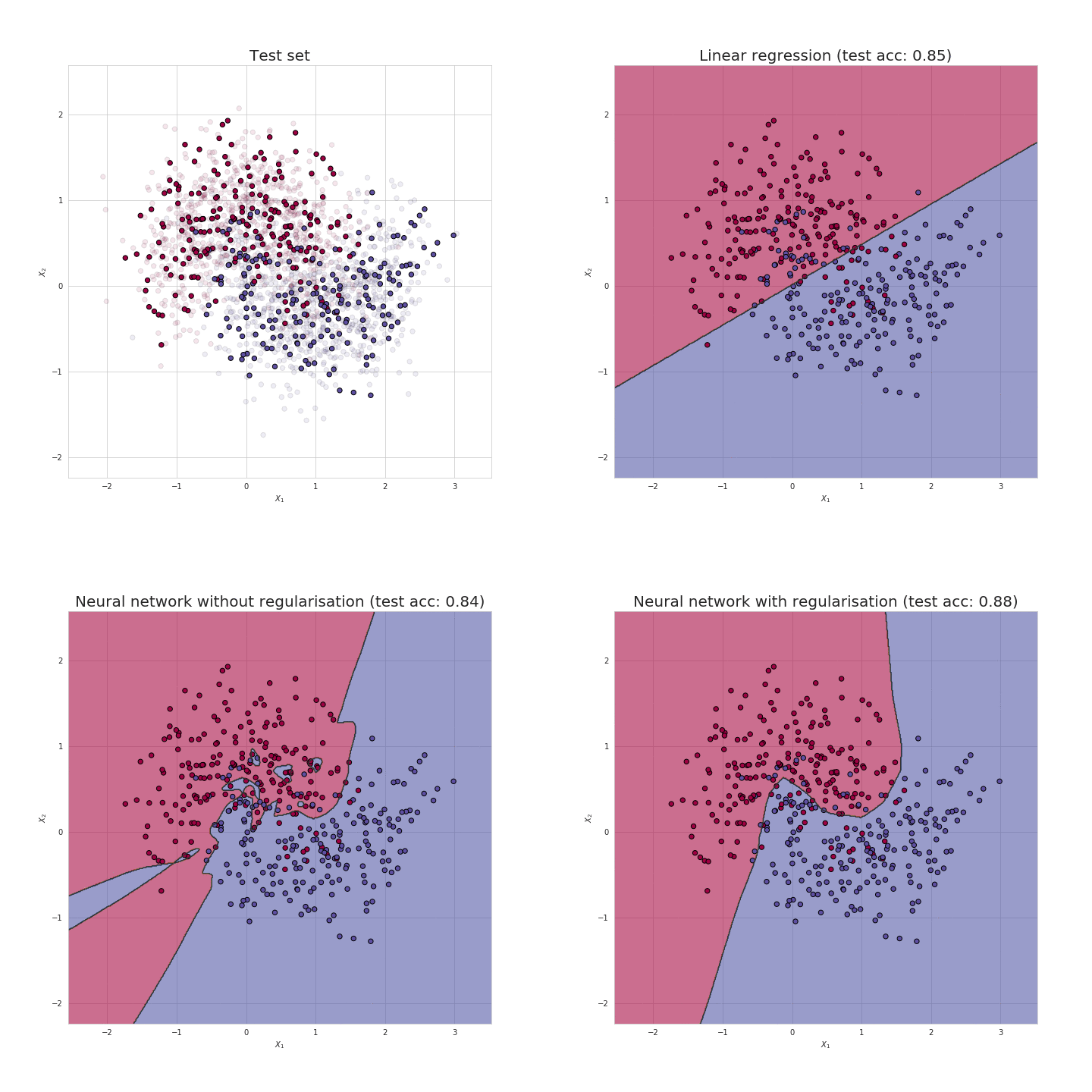
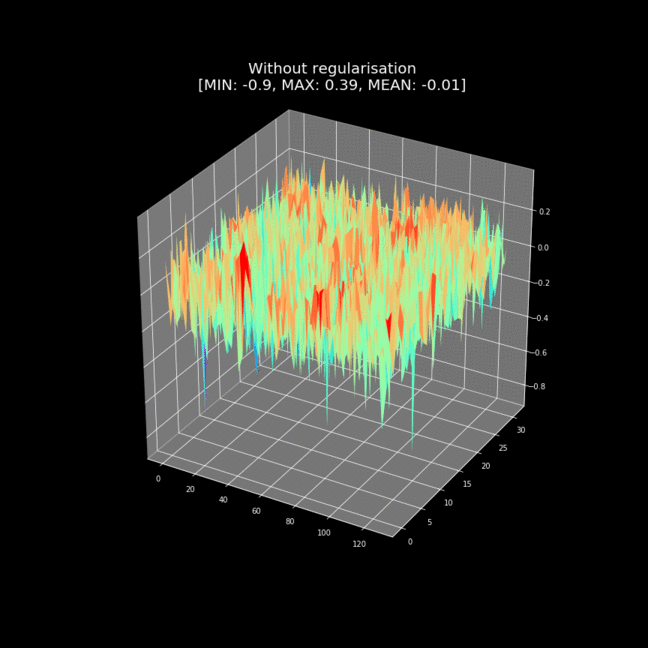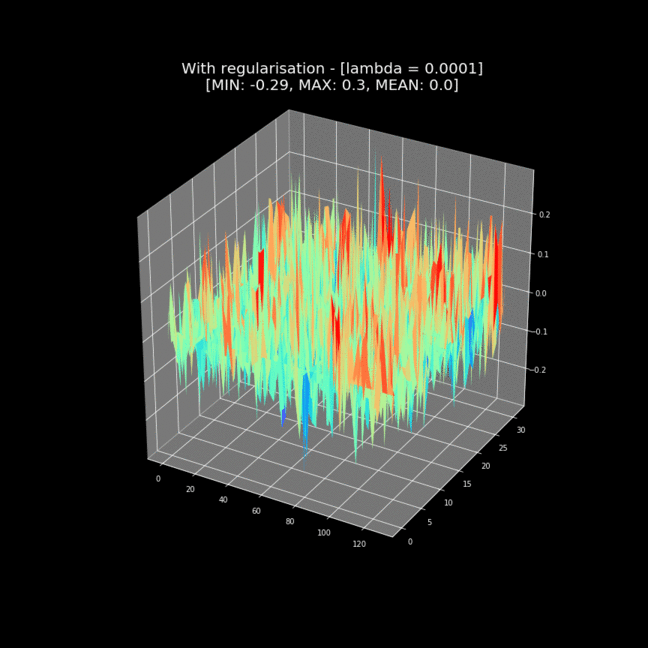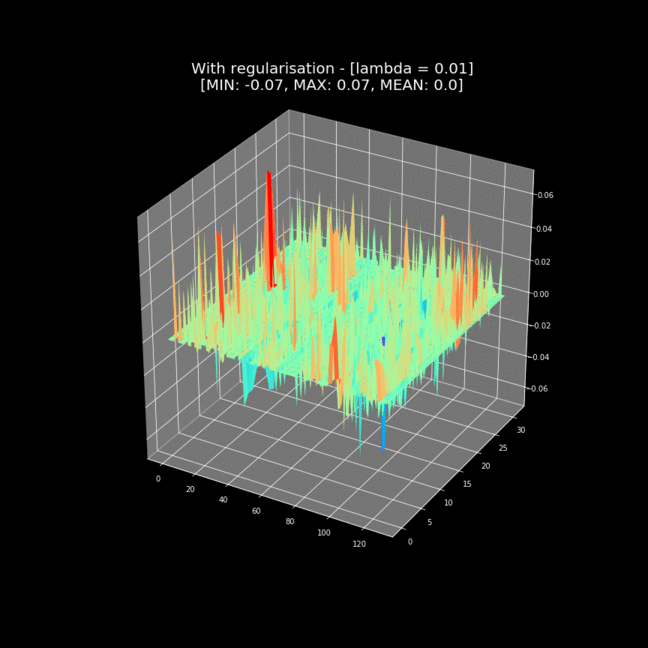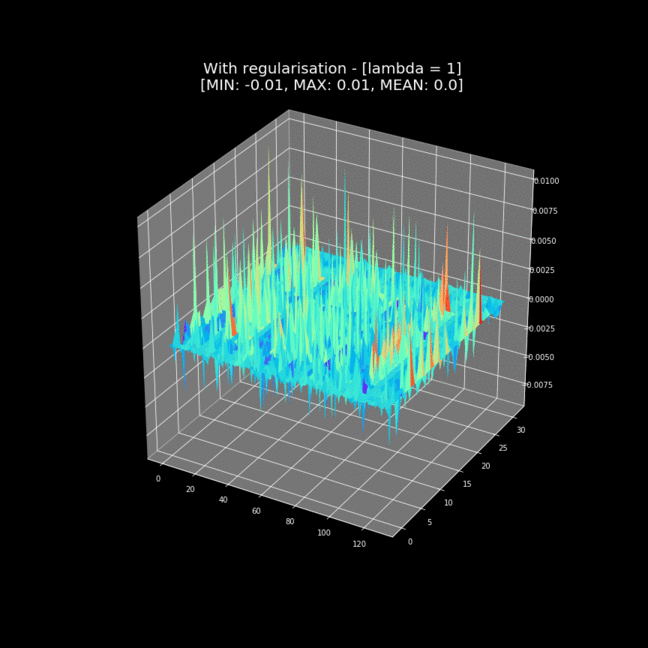
L1 or L2 Regularization
How do neural networks learn?
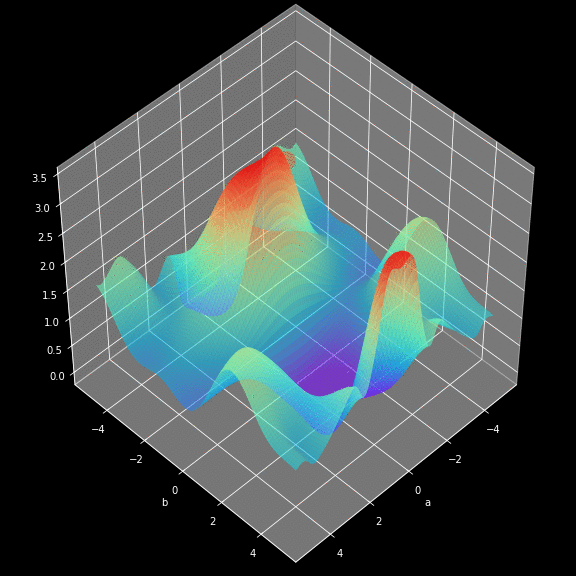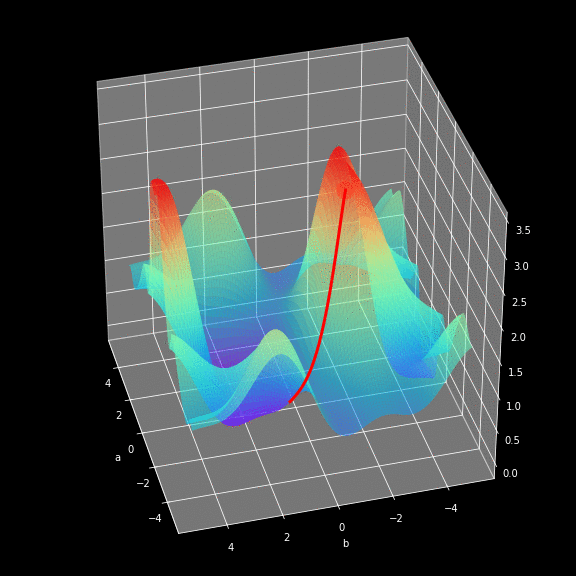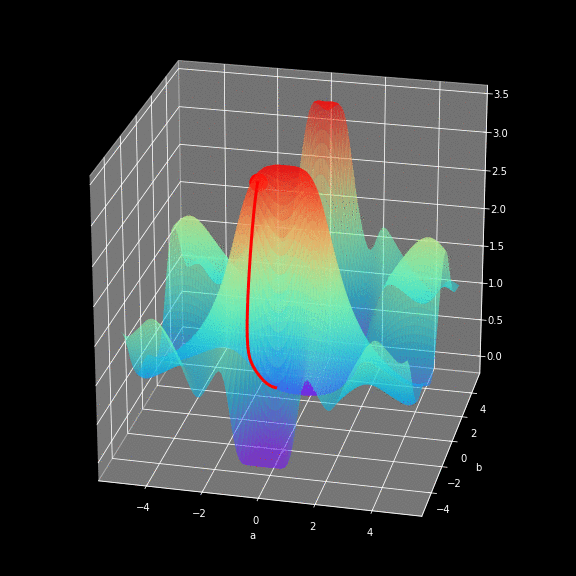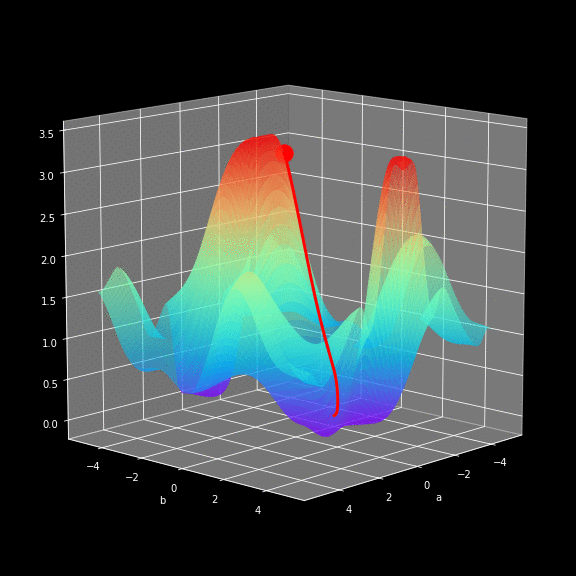
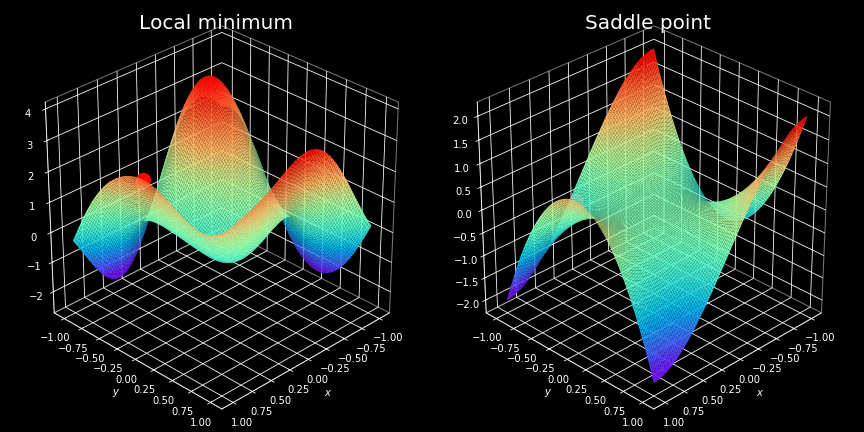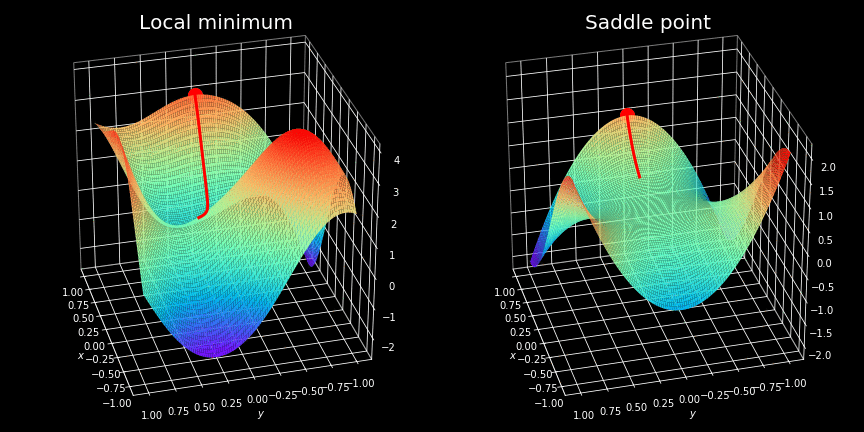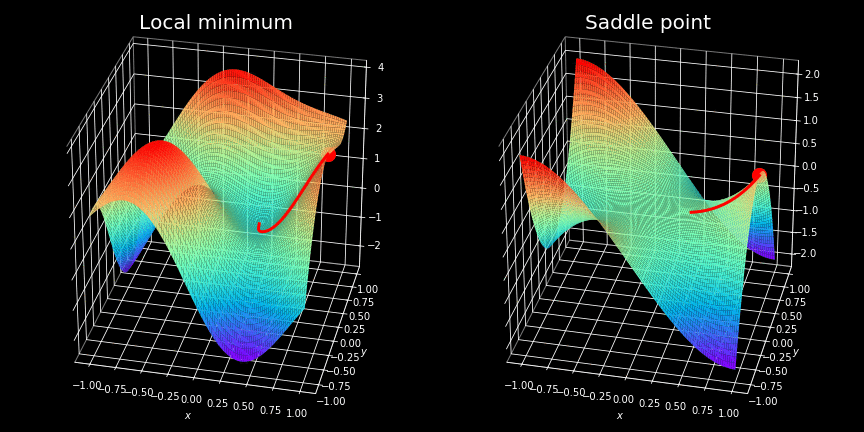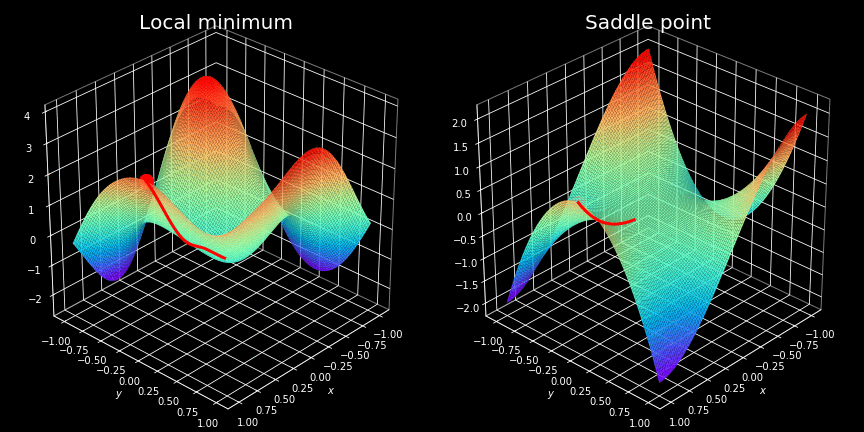
Critical Points
Backpropagation
Parameters adjust
$W^{[l]}=W^{[l]}-\alpha dW^{[l]}$
$b^{[l]}=b^{[l]}-\alpha db^{[l]}$
In Matrix Form
$dW^{[l]}=\frac{\partial L}{\partial W^{[l]}}=\frac{1}{m}dZ^{[l]}A^{[l-1]T}$
$db^{[l]}=\frac{\partial L}{\partial b^{[l]}}=\frac{1}{m}\sum_{i=1}^m dZ^{[l](i)}$
$dA^{[l-1]}=\frac{\partial L}{\partial A^{[l-1]}}=W^{[l]T}dZ^{[l]}$
$dZ^{[l]}=dA^{[l]}*g^{'}(Z^{[l]})$